General
Random Portfolios
- What are random portfolios?
- How can random portfolios be used?
- How can something random produce more information than other performance measurement techniques?
- Are there other names for “random portfolio”?
Optimization
- Don’t portfolio optimizers give wild answers?
- Does Portfolio Probe perform robust optimization
- Why is the function called trade.optimizer rather than portfolio.optimizer?
- Why use a genetic algorithm?
- Aren’t genetic algorithms slow?
- Are constraints on the number of assets in the portfolio and the number of assets traded really useful?
- Why not just impose round lotting after the optimization?
- When shouldn’t I use Portfolio Probe for optimization?
General
Why use the R (or S) language?
The S language (R or S-PLUS) provides a suitable and flexible environment in which to do tasks related to portfolios. S is arguably the best computing environment available for data analysis, which is a key component of fund management. More details on the advantages of the S language can be found in An Introduction to the S Language.
Spreadsheets, on the other hand, are stretched to the breaking point when doing optimization, and would be extremely unwieldy for random portfolios. See Spreadsheet Addiction.
The S language is of particular value when using random portfolios since this usually generates a lot of data that then needs to be summarized — just what S was made for.
back to top
What kind of risk model is used in Portfolio Probe?
Any risk model can be used — the choice is up to the user.
No risk models are included in Portfolio Probe. However, the Portfolio Probe User’s Manual points to ways that you can create your own statistical models given a matrix of returns.
A feature of Portfolio Probe is that multiple variances can be used for an optimization. So, for example, you could include both a commercial fundamental risk model and a statistical factor model that you’ve estimated yourself. Or, probably more useful, one or more variances created under the assumption of market troubles — for instance risk fraction constraints could be imposed on these variances.
Random Portfolios
What are random portfolios?
The idea of random portfolios is that they are a random sample of all of the portfolios that satisfy a given set of constraints.
Suppose that our universe of assets is the stocks contained in the S&P 500. We might want to request 1000 long-only portfolios that have a value between one million dollars and 1.01 million dollars, no asset has a weight greater than 5%, and there are between 30 and 60 assets in the portfolio.
So out of all the portfolios that might be constructed from those 500 assets, we are selecting portfolios that have a specific set of attributes. Notice that utility is not involved. Typically part of the point of using random portfolios is that we are ignoring perceived utility when we select the portfolios.
More on random portfolios can be found at Random Portfolios in Finance.
How can random portfolios be used?
There are a number of uses. See Applications of random portfolios.
How can something random produce more information than other performance measurement techniques?
It sounds paradoxical, but there is a simple explanation. The random portfolios are using more information from the market than peer groups or benchmarks.
Although each random portfolio only carries a little information, we use a lot of them. Think of how a blind person uses a cane. Each tap of the cane provides a minute amount of information, but a lot of taps builds up a picture of the terrain.
A benchmark uses the returns from the entire universe of assets, but we only see an aggregation of the returns. Random portfolios use the returns of the individual assets.
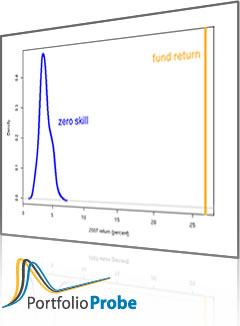
There are a few advantages that random portfolios have over peer groups in terms of information. Perhaps most important is that when we compare a fund to random portfolios, we know what we are doing — we know that the random portfolios have zero skill. We have no idea what skill level the peers have. Also we can generate as many random portfolios as we like, the number of peers in the group depends on how loosely we want to categorize funds. With random portfolios, we can specialize the constraints to the particular fund.
In performance measurement we want to distinguish skill from luck. Random portfolios show us what luck looks like, and what doesn’t look like luck is probably skill.
Are there other names for random portfolio?
Using random portfolios is often called “Monte Carlo” or “Monte Carlo simulation”. However, the term “Monte Carlo simulation” more frequently refers to simulating portfolios into the future than to the more factual activity of creating random portfolios.
In the realm of performance measurement there is often the image of a monkey and/or the throwing of darts.
Optimization
Don’t portfolio optimizers give wild answers?
A portfolio optimizer that is given naive inputs will produce solutions that could be financial disaster. However, automobiles have not been abandoned because they crash when left to run down hill on their own.
When reasonable constraints and (especially) trading costs are used, an optimization is likely to provide better answers than can be found by other means — and possibly with less effort than the alternatives. An optimizer can provide improved risk management, making the fund manager’s return predictions more valuable.
Utility-free optimization will not give wild answers. It will always move towards your target portfolio.
Does Portfolio Probe perform robust optimization?
There is an unfortunately large number of meanings for the word “robust” (even when coupled with “optimization”), but let’s assume the meaning relates to the fact that the inputs to an optimization are not known explicitly.
A typical optimization depends on a variance matrix and expected returns of the assets. The variance matrix is a prediction and always contains some noise. The expected returns contain a very large amount of noise. A standard optimization tells you the best trade to make if the variance matrix and the expected returns were known exactly.
Robust optimization (in the current sense) does some modification to take account of the noise in the inputs. Portfolio Probe has no special modes nor features for robust optimization. So in that sense the answer to the question is, “no”.
However, a form of robust optimization can be done with Portfolio Probe (and most other optimizers) quite simply.
Assume the most common situation: that we have a portfolio in place and we are considering some trading to improve it. Let’s look at two extremes. In the first case, your expected returns and variance matrix are known perfectly. Here you should do the trade that the optimizer gives you. In the second case the inputs are given to you by someone who is completely delusional. In this case, you should completely ignore the results of the optimizer — that is, you should trade nothing. The real case will be somewhere between these two extremes. Thus you should go part way towards where the optimizer tells you to go. You can achieve that by either increasing trading costs or imposing a turnover constraint.
Why is the function called trade.optimizer rather than portfolio.optimizer?
Although the popular phrase is “portfolio optimization”, it really is the trade and not the portfolio that we want to optimize. There has been a substantial amount of misdirected effort due to not realizing that the trade, and not the portfolio, is the object of optimization. By calling the function “trade.optimizer”, it is hoped that such misdirection will be reduced.
Why use a genetic algorithm?
Primarily so that the real problem of interest is solved. The approach in most other portfolio optimization software is to change the problem so that it fits the optimizer.
A portfolio optimization program based on a genetic algorithm easily allows multiple integer constraints, nonlinear trading costs and modifications to the utility.
A random algorithm, such as a genetic algorithm, is essential in order to generate random portfolios.
Aren’t genetic algorithms slow?
Yes and no.
The original genetic algorithm is horribly slow and inefficient. Algorithms that are too closely based on the original are also slow. The algorithm that powers Portfolio Probe has been specially adapted to the problem at hand and performs quite well. Much of its speed is due to not being purely genetic — other techniques are employed as well.
Many genetic algorithms for portfolio optimization merely use a genetic algorithm to optimize over one integer constraint and use a quadratic programming algorithm to actually do the optimization. This will also be slow, and fails to take full advantage of the flexibility that a genetic algorithm can provide.
Are constraints on the number of assets in the portfolio and the number of assets traded really useful?
When generating random portfolios, these constraints are fairly typically what you actually want. In optimization they are often really just a convenient shortcut for threshold constraints. A threshold constraint says that a trade or a portfolio position needs to be of at least a certain size if it exists at all. So, yes they are useful but imposing threshold constraints might be what you really mean.
Why not just impose round lotting after the optimization?
The implication is that there is little difference between round lotting within the optimization process or doing it just once afterwards. In many cases this is true. However, the cost of coercing to round lots within the algorithm is minimal, and there are times when it does matter.
Some optimizations involve assets with large prices relative to the size of the trade, in which case the round lotting will be important. Examples of large prices include some futures and a few equities. Alternatively the size of the trade can be small, such as when optimization is performed continuously. Given that real-time optimization can easily be done with Portfolio Probe, this could be an important consideration.
When shouldn’t I use Portfolio Probe for optimization?
(Often the question is phrased quite differently.) If you have a utility that is amenable to quadratic programming (that is, some variation of mean-variance), you don’t have any integer (or threshold) constraints, and speed is important, then optimization with Portfolio Probe is not your best choice.