There are (at least) three general areas for which random portfolios are useful:
- Performance
- Risk
- Quant
Performance
The concepts of “benchmark” and “peer group” have been extensively used in performance. Random portfolios are superior because:
- they are more specific to a particular fund
- they extract more information from the market
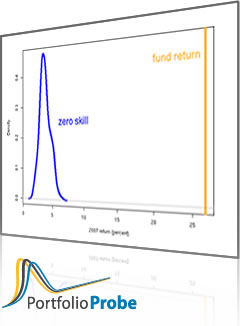
The picture is an example of random portfolios in action to assess performance. The red line is the fund return during the year. It is in the left tail of the distributions, so an indication that the fund underperformed during the year. But there is much more information represented — you can learn what it is from:
more about Performance Measurement
Other performance applications include:
more about Performance Attribution
more about Portfolio Construction Process Attribution
Risk
Create realistic portfolios with which to test and compare risk models.
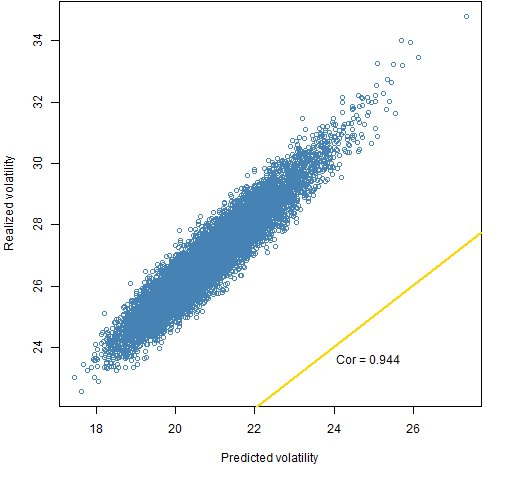The figure shows the relationship between predicted and realized volatility for a certain risk model, period and set of constraints.
Quant
There are a number of specific uses of random portfolios that have been advanced within the quant realm. There are undoubtedly even more uses that have not yet been thought of.
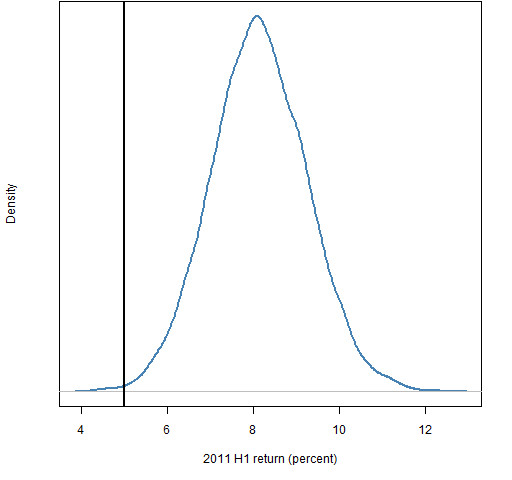The figure shows the returns of portfolios that — among their constraints — have beta essentially equal to one (0.99 to 1.01) compared to the index (S&P 500). The black line is the return of the index.
Important uses of random portfolios include calibrating backtests, and understanding the effect of the constraints that are placed on funds.
more about Test a Trading Strategy
more about Evaluate Constraint Bounds
more about Quantitative Research
