How good is the current opportunity to pick stocks relative to the past?
Idea
The more stocks act differently from each other relative to how volatile they are, the more opportunity there is to benefit by selecting stocks. This post looks at a particular way of investigating that idea.
Data
Daily (log) returns of 442 large cap US stocks with histories back to the start of 2004 were used.
The ratio
Consider a window of returns over a certain period and of a certain universe of assets. We can get a measure of the variability of these returns in two ways:
- find the standard deviation across the universe for each time point, and then average those numbers (variability across assets)
- average the returns at each time point and then get the standard deviation of those averages (variability across time)
The first thought for many people is that these should give the same number. They don’t.
The bigger the first number is relative to the second, the more possibility there is to profitably select assets. If the second is large relative to the first, then the market is volatile but all the assets tend to move together.
The “opportunity ratio” is the first number divided by the second. Below are pictures of how the ratio changes over time for rolling windows of 200 days and 60 days.
Results
Figures 1 and 2 show the opportunity ratio through time.
Figure 1: 200-day rolling window of the opportunity ratio. 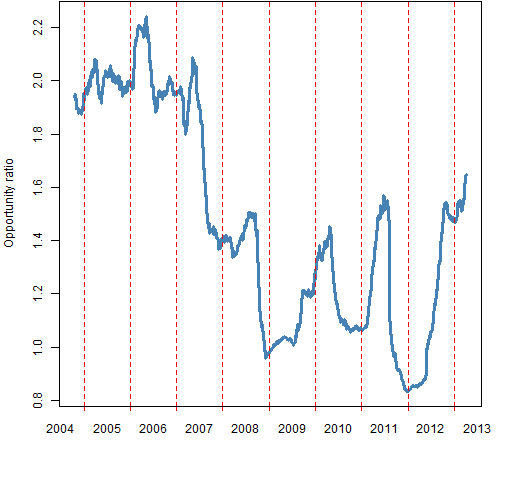
Figure 2: 60-day rolling window of the opportunity ratio. 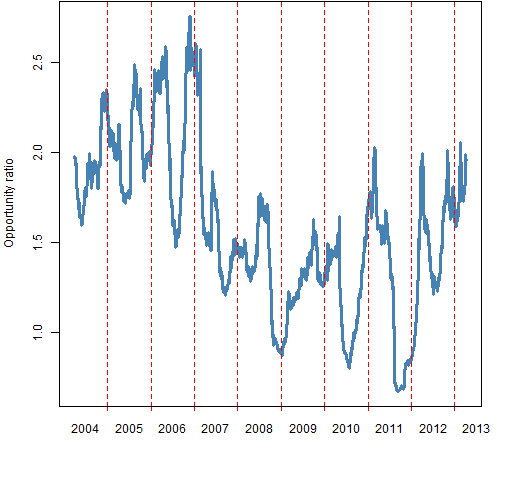 These pictures show (at least) two things:
These pictures show (at least) two things:
Almost always the ratio is bigger than 1. This supports the view that “the market” is an over-simplification — these stocks have a tendency to march to their own drummer.
There is some hope that the ratio is recovering from the financial crisis.
Estimating variability
The final value for the 200-day ratio is 1.65, and 1.96 for the 60-day ratio. The last day in the data is 2013 April 5. We might like to know how variable these numbers are — they are, afterall, estimates based on data.
A common way of getting a sense of the variability of a statistic is to use the statistical bootstrap. A complication here is that we want to account for variability due to both the time points and the assets. That’s okay — we can do resampling on both of those simultaneously.
Figures 3 and 4 show the bootstrap distributions for the two final ratios.
Figure 3: bootstrap distribution of the opportunity ratio for the 200 days ending on 2013 April 5. 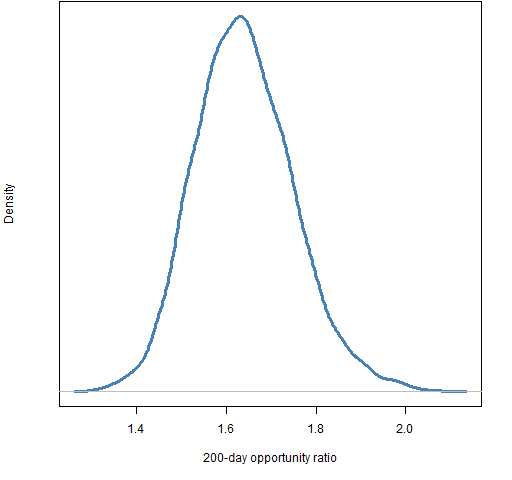
Figure 4: bootstrap distribution of the opportunity ratio for the 60 days ending on 2013 April 5. 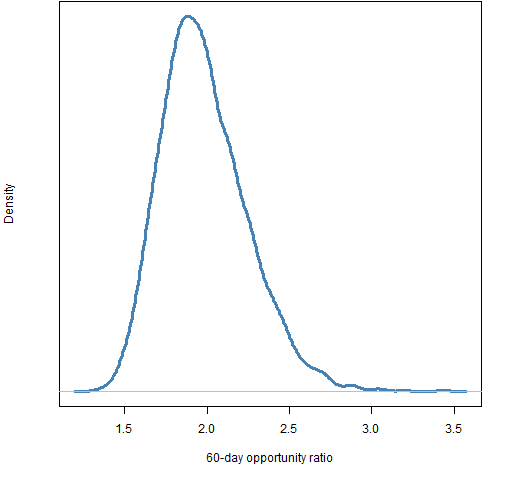
Most of the variability seems to come from resampling the days rather than the assets. There are more assets which is probably at least part of the reason.
Summary
Stock-picking opportunity seems to be good relative to the rest of the post-crisis period.
This is a simple, but perhaps reasonable approach to exploring selection opportunity.
Appendix R
Computations were done in R.
compute the ratio
A function to compute a single ratio is:
pp.sdratioSingle <- function(retmat)
{
# single computation of opportunity ratio
# Placed in the public domain 2013 by Burns Statistics
# Testing status: untested
mean(apply(retmat, 1, sd)) / sd(rowMeans(retmat))
}
A function to compute rolling windows of the ratio is:
pp.sdratio <- function(retmat, window=200)
{
# rolling window computation of opportunity ratio
# Placed in the public domain 2013 by Burns Statistics
# Testing status: untested
averet <- rowMeans(retmat)
vol <- rollapply(averet, FUN=sd, width=window,
align="right")
daycross <- apply(retmat, 1, sd)
cross <- rollapply(daycross, FUN=mean, width=window,
align="right")
names(vol) <- names(cross)
list(volatility=vol, cross.sd=cross, ratio=cross/vol,
call=match.call())
}
This latter function is used like:
opportun <- pp.sdratio(diff(log(univclose130406)))
time plot
The function used to create Figures 1 and 2 is pp.timeplot which you can put into your R session with:
source("https://www.portfolioprobe.com/R/blog/pp.timeplot.R")
bootstrap
A function that will return one matrix that has the original rows and/or columns bootstrapped is:
pp.matrixboot <- function(x, rows=TRUE, columns=TRUE)
{
# bootstrap sampling on rows and/or columns of a matrix
# Placed in the public domain 2013 by Burns Statistics
# Testing status: untested
dx <- dim(x)
if(rows) {
rsub <- sample(dx[1], dx[1], replace=TRUE)
} else {
rsub <- TRUE
}
if(columns) {
csub <- sample(dx[2], dx[2], replace=TRUE)
} else {
csub <- TRUE
}
x[rsub, csub]
}
This was used like:
orboot200 <- orboot60 <- numeric(5000)
for(i in seq_along(orboot200)) {
orboot200[i] <- pp.sdratioSingle(pp.matrixboot(lateret))
}
Great post Patrick, I have been looking for an easy way to measure that for some time. Have been looking at Antti Petajisto’s Active Share measure but it is just too data intensive ( requires position level data for both fund and benchmark ) to be easily implementable. Your more global method plus a comparison with some passive and active funds should help shed some light on any cyclicality that may exist. Might well be helpful in timing an active / passive regime change.
Your analysis seems to be similar in some regards to ANOVA but does seem to differ computationally. If you were to use ANOVA, then you could look at the CDF percentile of the F statistic and use that instead of what you are proposing. This would take into account the degrees of freedom.
In addition, Kritzman et al mentioned a few statistics similar in ilk to what you propose in their paper titled ‘Principal Components as a Measure of Systemic Risk.’ I don’t favor their primary Absorption Ratio as their ‘1/3’ rule for eigenvalues is arbitrary, but have spent some time looking at their AR_Herfindahl index listed in the appendix. Also, Varadi et al have some interesting metrics in their ‘The Minimum Correlation Algorithm’ paper as well: would like to have seen more rigor in their approach, but they provide a lot of information and code.
All in all, what is of interest is the off-diagonal of the covariance matrix: finding something that has rigor and robustness would be beneficial. Thanks for your interesting exposition on the subject: I think there is a lot of value in this type of analysis from a lot of viewpoints. I.e. when to alternate between active fund managers, assuming they have skill, and an index (although if it is market cap weighted, then it really is an active fund).
Robert,
It was perceptive to see that this is like ANOVA. I think we’d want to estimate variance components (REML and all that) if we moved in that direction. That would certainly lose the simplicity of the current analysis, but it might give some interesting results.
Great analysis.
Regards,
Shunchiao (Josh) hsu
“The more stocks act differently…, the more opportunity there is to benefit by selecting stocks.”
I am not sure about this, because the more stocks act differently, the higher the probability of selecting the “wrong” stocks. With “stock-picking opportunity”, people usually refer to “positive results” from stock picking. But an increase in dispersion will increase the upside as well as the downside opportunities, most likely in a way such that expected stock-picking opportunities are unaffected. This is a statistical argument. It reminds me of the question whether there exists extraterrestrial life. The larger the universe, the higher the probability of existence, but at the same time the lower the probability of ever meeting them. There also exist economic arguments which imply that more dispersion does not necessarily result in an increase in “opportunities” (in short: search costs).
Andreas,
I take it as given that if you have opportunity to outperform, then you also have opportunity to underperform. I don’t see how there can be opportunity if everyone will have the same results.