Winsorization replaces extreme data values with less extreme values.
But why
Extreme values sometimes have a big effect on statistical operations. That effect is not necessarily a good effect. One approach to the problem is to change the statistical operation — this is the field of robust statistics.
An alternative solution is to just change the data. You can then use whatever statistical procedure you want.
In my experience in finance only mildly robust statistics (and hence only mildly winsorized data) are called for. There seems to be a surprising amount of information in the tails of financial returns.
Trimming
There is an alternative to winsorization, which is just throwing out the extreme values. That is called “trimming”. The mean function in R has a trim argument so that you can easily get trimmed means:
> mean(c(1:10, 300))
[1] 32.27273
> mean(c(1:10, 300), trim=.05)
[1] 32.27273
> mean(c(1:10, 300), trim=.1)
[1] 6
Trimming removes a certain fraction of the data from each tail.
Winsorizing — one way
One approach to winsorization is just to copy trimming, but replace the extreme values rather than throw them out. Here is an R function that does this:
> winsor1
function (x, fraction=.05)
{
if(length(fraction) != 1 || fraction < 0 ||
fraction > 0.5) {
stop("bad value for 'fraction'")
}
lim <- quantile(x, probs=c(fraction, 1-fraction))
x[ x < lim[1] ] <- lim[1]
x[ x > lim[2] ] <- lim[2]
x
}
Figures 1 and 2 show this function in action.
Figure 1: The winsor1 function with some normally distributed data. 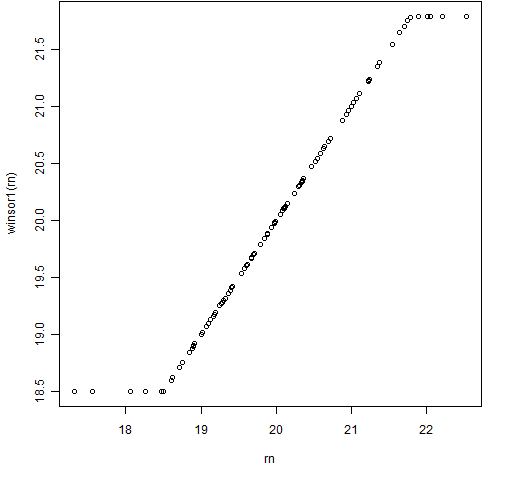
Figure 2: The winsor1 function with some Cauchy distributed data. 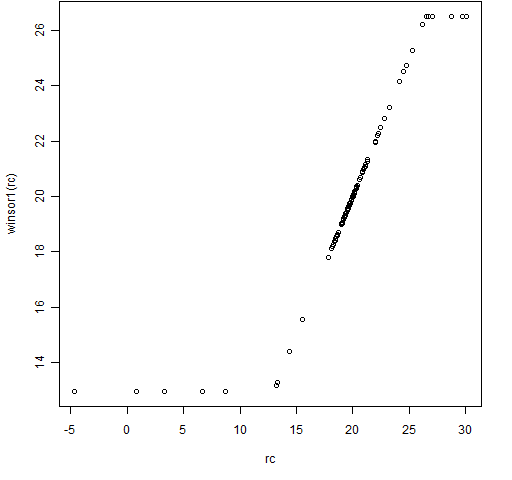
Winsorizing — another way
Another approach to winsorization is to try to just move the datapoints that are likely to be troublesome. That is, only move data that are too far from the rest. Here is such an R function:
> winsor2
function (x, multiple=3)
{
if(length(multiple) != 1 || multiple <= 0) {
stop("bad value for 'multiple'")
}
med <- median(x)
y <- x - med
sc <- mad(y, center=0) * multiple
y[ y > sc ] <- sc
y[ y < -sc ] <- -sc
y + med
}
Figures 3 and 4 show the results of this function using the same data as in Figures 1 and 2.
Figure 3: The winsor2 function with some normally distributed data. 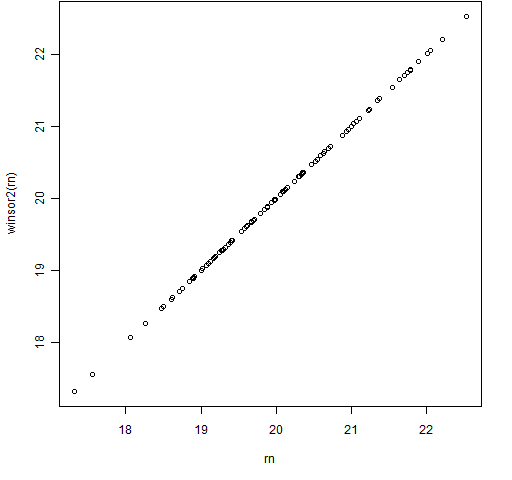
Figure 4: The winsor2 function with some Cauchy distributed data. 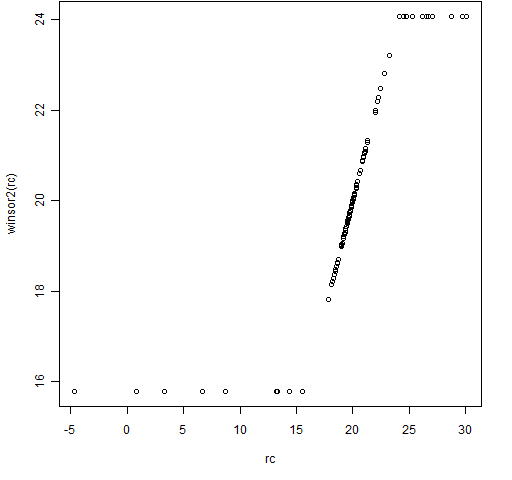
Comments
I think the second form of winsorization usually makes more sense. In the examples the normal data are not changed at all by the second method and the Cauchy data look to be changed in a more logical way.
Production quality implementations of the R functions would probably include an na.rm argument to deal with missing values.
I really like your winsor2() function. Especially the “multiple” adjustment.
#Very little cutoff. 100 data points
x <- rnorm(100)
plot(x, winsor2(x, 3))
#Obvious cutoff. 10000 data points
x <- rnorm(10000)
plot(x, winsor2(x, 3))
#Very little cutoff. 10000 data points
x <- rnorm(10000)
plot(x, winsor2(x, 5))
Good point that what you want to do may depend on how much data you have.
You could get a little more clarity and speed by replacing
y[ y > sc ] <- sc
y[ y < -sc ] <- -sc
with something like
y <- pmin(pmax(y, -sc), sc)
Rob,
Thanks. Clarity is an important consideration.
Have you tried timing the two? My intuition says that the subscripting would be faster. But that should almost surely take a backseat to clarity since the time difference is going to be small in any event.
My take on clarity is the reverse of yours as well. I’d be keen to put it to a vote on which is more clear to the rest of the R world.
It looks like you’re right about indexing being faster. Regarding clarity, this is an idiom I use all the time so it’s instantly recognizable to me. It’s like a low level design pattern. I find these are especially important in R, given its infernal side.
Thanks!
Rob,
Thanks for the timing report.
We still don’t have any more clarity on clarity.
Hi Pat,
My background is biology so could you please tell me the meaning of the “multiple” option in winsor2 function?
Thanks
Safa
Safa,
multipleis multiplying the computed value ofmad(a robust estimate of the standard deviation). So whenmultipleis 3, we are pulling values in that are farther than 3 (estimated) standard deviations from the center.An improvement to the function would be to add a
centerargument that defaulted to the median.thanks, i get it now