How to visualize luck when looking for skill.

Quantitative Finance just published the paper Dicing with the market: randomized procedures for evaluation of mutual funds by Francesco Lisi.  Here is the working paper version.

This paper explains one way of using random portfolios to do performance measurement of investment funds.  It includes performance measures on several Italian mutual funds.

Strong points

Confronting luck

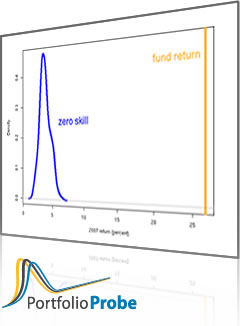
The paper states (rather clearly I think) why you need to understand what luck looks like in order to see if a fund exhibits skill.

It highlights advantages that random portfolios have over using benchmarks and peer groups for performance measurement.

Individual fund

It points out that this measures an individual fund on its own.  There is no need for a cohort of funds.  From a practical point of view this is quite important.  It is of little value to an investor to know how many skillful funds there are but not which ones.

Model free

The paper identifies another key advantage: that there is no model, and hence no model risk.  Only the reality of market data is used.

Semi-random portfolios

Some experiments are shown where the selected fraction of above average performing assets is manipulated.  Returns are dramatic.  It is a convincing indication of the ignorance of even the best money managers.

Multi-time

The skill of a fund is unlikely to be constant, and certainly the evidence of skill will be non-constant.  Some scheme or schemes are needed to think about skill over different time periods.

The paper firmly addresses this issue.

Weak points

Equal weights only

The random portfolios that are generated are very simplistic.  They are equal weightings of a certain number of randomly selected assets out of the universe.

This would be a strong point if the equal-weight distribution looked a lot like the distributions using more realistic constraints.  But we don’t know how different they are.  It would be an easy exercise to see how different the distributions are, but as far as I know no one has done that yet.

Statistical straitjacket

The paper fixes on the 95% quantile of the random distribution as the dividing line between skill and luck.  This comes from the typical use of a 5% type I error in statistics.

I prefer to think in terms of p-values since we are doing this fund by fund.  Actually I think an informal Bayesian approach is what really should be used.  The random portfolio results should be combined with other information to arrive at a decision about the fund.

Multi-time

While I think it great that the paper confronts the problem concerning time, I’m not convinced by the solutions that the paper uses.

The time frame over which a fund should be judged depends on the fund’s typical holding period.  If a fund holds assets on the order of minutes, then it is going to be fine to judge the fund every day.

Daily judging of a fund that holds assets for months doesn’t make sense to me.  The paper doesn’t really do this, but it sort of does.

Past performance of mutual funds is often reported for 1 year, 3 years and 5 years.  It seems reasonable to report exhibited skill for those time frames.  For an academic study these could be given as of the start of each year in the data.

Static portfolios

The paper notes that random portfolios allow analysis specialized to a single fund, but it doesn’t use (or discuss) a very powerful form of specialization.

Once we have selected a time period for the analysis, we can condition on the positions of the fund at the start of the time period and the turnover of the fund to create an extremely effective analysis of performance.  This is called the shadowing method.

As the paper notes, not all information may be known outside the fund manager to do an exact analysis with random portfolios.  That is true of static portfolios, and more true of the shadowing method.  However, reasonable guesses can be used if the fund manager can’t be convinced to publish analyses of its funds.